Del ciclo: «La relación de las diversas ramas de las ciencias naturales con la astronomía»

Rudolf Steiner — Stuttgart, 9 de enero de 1921

English version

 

Mis queridos amigos,

Ahora hemos llegado a un punto en nuestros estudios desde el cual debemos proceder con extrema precaución, para ver dónde existe el peligro de permitir que nuestro pensamiento se aparte de la realidad y también para ver cuándo estamos evitando este peligro, manteniéndonos dentro del límites de lo que es real.

La última vez, sugerimos la comparación de dos hechos: la aparición dentro del sistema planetario de los fenómenos cometarios y ¡ay! dentro del sistema planetario, aunque tal vez no tenga la misma relación con ella todo lo que observamos en los fenómenos de la fertilización. Sin embargo, para llegar a ideas sobre esto que estén justificadas, primero debemos ver si es realmente posible encontrar conexiones entre dos cosas tan separadas, con las cuales nos enfrentamos en el mundo externo de los hechos. En el método científico, no haremos progresos reales, a menos que podamos referirnos de un reino de hechos a otro, manifestando algo de naturaleza similar y, por lo tanto, conduciéndonos.

Hemos visto cómo, por un lado, tenemos que usar el elemento de figura y forma, el matemático, y luego cómo nos vemos impulsados ​​una y otra vez a llegar a un acuerdo de una forma u otra con el aspecto cualitativo, para de alguna manera encontrar un enfoque cualitativo. Y así, hoy traeremos algo que surge con respecto al hombre si uno realmente estudia a este hombre, que es, después de todo, una imagen de los fenómenos celestiales —como las muchas declaraciones en estas conferencias pueden permitirnos deducir. Sin embargo, todavía tenemos que establecer de qué manera es esta imagen. Si esto es lo que es, primero debemos obtener una comprensión clara del hombre mismo. Debemos entender la imagen de la que pretendemos comenzar —comprender su perspectiva interna. Al igual que al mirar una pintura, uno debe saber lo que significa un escorzo, y así sucesivamente, para pasar de la imagen a las relaciones espaciales reales y relacionar la imagen con lo que representa en la realidad, entonces, si nos acercáramos a la realidad en el universo, interpretándolo a través del hombre, primero debemos ser claros acerca del hombre. Ahora, como ser humano, es extraordinariamente difícil acercarse al ser humano con ideas palpables. Por lo tanto, me gustaría presentar hoy ante sus almas lo que podría llamar imágenes de pensamiento «palpablemente impalpables» que surgen de fundamentos bastante simples, ideas con las cuales la mayoría de ustedes probablemente ya están bien familiarizados, pero que sin embargo debemos presentar ante nuestras mentes con una cierta conexión. Estas ideas, que en parte parecen ser bastante fáciles de comprender y, más allá de ciertos límites, de eludir a nuestra comprensión, nos brindarán un medio de orientación en el esfuerzo por afianzar el mundo exterior a través de las ideas.

Puede parecer algo forzado el seguir enfatizando la necesidad de referirse de nuevo a la vida del hombre de la imaginación pictórica para comprender los fenómenos de los cielos. Pero, después de todo, es obvio que, por mucho cuidado que pongamos en describir los fenómenos celestiales, tenemos, para empezar, nada más que una forma de imagen óptica, impregnada de pensamientos matemáticos. Lo que nos ofrece la astronomía tiene fundamentalmente el carácter de una imagen. Para estar en el camino correcto, por lo tanto, debemos preocuparnos por el surgimiento de la imagen en el hombre, de lo contrario no obtendremos una relación verdadera con lo que la astronomía puede decirnos. Y, por lo tanto, me gustaría proceder hoy con algunas matemáticas bastante simples y mostrarles cómo, en un dominio diferente al que fuimos conducidos a través de las proporciones de los períodos de revolución de los planetas, aparece dentro de las propias matemáticas este elemento de lo incomprensible, lo impalpable. Nos encontramos con ello cuando, en cierta conexión, estudiamos curvas bastante familiares. (Como dije, muchos de ustedes ya saben lo que voy a describir, solo quiero aclarar el tema hoy desde un aspecto particular).

Consideren la elipse, con sus dos focos A y B, y saben que una definición de la elipse es que para cualquier punto M de la curva, la suma de sus distancias (a + b) desde los dos focos permanece constante. Es característico de la elipse, que la suma de las distancias de cualquiera de sus puntos, desde dos puntos fijos, los dos focos, permanezca constante (Fig. 1).

 

Luego tenemos una segunda curva, la hipérbola (Fig. 2). Saben que tiene dos ramas. Se define en que la diferencia de las distancias de cualquier punto de la curva de los dos focos, (b – a) es una magnitud constante. En la elipse, entonces, tenemos la curva de la suma constante, en la hipérbola, la curva de la diferencia constante, y ahora debemos preguntarnos: ¿Cuál es la curva del producto constante?

A menudo he llamado la atención sobre esto: la curva del producto constante es la llamada Curva de Cassini (Fig. 3). La encontramos cuando, teniendo dos puntos, A y B, consideramos un punto M con respecto a sus distancias de A y B, y establecemos la condición de que las dos distancias AM y BM multiplicadas deberían ser de una magnitud constante. En aras de la simplicidad en el cálculo, llamaré la magnitud constante b2 y la distancia AB =2a. Si tomamos el punto medio entre a y b como el centro de los ejes de un sistema de coordenadas y calculamos las ordenadas para cada punto que cumple estas condiciones, tomamos C como el centro del sistema de coordenadas y dejamos que el punto cuya ordenada llamaremos “y” se mueva alrededor para que en cada punto de la curva AM x BM = b2, obtengamos la siguiente ecuación. (Solo les daré el resultado, por la sencilla razón de que todos pueden hacer fácilmente el cálculo por sí mismos; se encuentra en cualquier libro de texto matemático relacionado con el tema). Encontramos para “y” el valor:

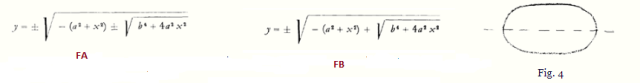
Teniendo en cuenta aquí que no podemos usar el signo negativo porque deberíamos tener una “y” imaginaria, y considerando por lo tanto solo el signo positivo, tenemos (FB). Si luego dibujamos la curva correspondiente, tenemos una curva, bastante parecida pero no idéntica a una elipse, llamada curva de Cassini (Fig. 4). Es simétrico a la izquierda y derecha del eje de ordenadas y alrededor y debajo del eje de abscisas.

Pero ahora, esta curva tiene varias formas, y para nosotros, en cualquier caso, esto es lo importante. La curva tiene diferentes formas, según si b, como lo he tomado aquí, es mayor que a, igual a a, o menor que a.

La curva que acabo de dibujar surge cuando b> a, y además cuando se cumple otra condición, a saber, que b también es mayor o igual que a.√2. Además, cuando b> a√2, hay una curvatura distinta arriba y abajo, si b = a√2, entonces en este punto arriba y abajo, la línea de la curva se endereza, se aplana tanto que casi se vuelve una línea recta (Fig. 4). Sin embargo, si b <a√2, entonces se cambia todo el curso de la curva y toma esta forma (Fig. 5). Y si b = a, la curva pasa a una forma bastante especial, cambia a esta forma (Fig. 6). Regresa a sí mismo, se atraviesa y sale del otro lado, y obtenemos la forma especial de la Lemniscata. La lemniscata, entonces, es una forma especial de la Curva de Cassini: estas curvas llevan el nombre de su descubridor. La forma particular asumida por la curva está determinada por la relación entre las magnitudes constantes que aparecen en la ecuación que caracteriza la curva. En la ecuación, solo tenemos estas dos magnitudes constantes, b y a, y la forma de la curva depende de la relación entre ellas.

 

 

Entonces es posible el tercer caso, que b <a. Si b <a, todavía podemos encontrar valores para la curva. Siempre podemos resolver la ecuación y obtener valores para la curva, ordenadas y abscisas, incluso cuando b es más pequeña que a, solo la curva experimenta otra metamorfosis. Para cuando b <a, encontramos dos ramas de la curva, que se parecen a esto (Fig. 7). Tenemos una curva discontinua. Y aquí llegamos al punto en que las matemáticas en sí nos confrontan con lo que llamé «palpablemente impalpable», algo que es difícil de comprender en el espacio. En el sentido de la ecuación matemática, esto no son dos curvas, sino una; es una curva única exactamente de la misma manera que todas estas son curvas simples (figuras 3 a 5). En esta (la lemniscata) ya hay una transición. El punto que describe la curva toma este camino, da una vuelta por debajo, corta su camino anterior aquí y continúa aquí (Fig.7). Aquí, debemos imaginar lo siguiente: si dejamos que el punto M se mueva a lo largo de esta línea, no se cruza simplemente de un lado a otro, no lo hace. Corre a lo largo del camino como en las otras curvas, describe una curva aquí, pero luego se las arregla para volver a subir aquí (Fig. 7) Verán, lo que lleva el punto a lo largo de la línea desaparece aquí en el medio. Si quieres entender la curva, solo puedes imaginar que desaparece en el medio. Si intentan formar una imagen mental continua de esta curva, ¿qué deben hacer?.

 

Es bastante fácil, imaginar curvas de este tipo (¡Solo digo esto entre paréntesis para el filisteo ordinario!) Pueden seguir imaginando puntos a lo largo de la curva y no encontrarán que la imagen se rompa. Aquí (en la lemniscata) hay que modificar la forma cómoda de simplemente dar vueltas y vueltas, pero aun así continúa constantemente. Puedes mantener la imagen mental. Pero ahora, cuando llegas a esta curva (Fig. 7), que no es tan común, y quieres imaginarla, entonces, para mantener la continuidad de la idea, tendrás que decir: el espacio ya no me da un punto de apoyo. Al cruzar a la otra rama en mi imaginación, a menos que rompa la continuidad y considere que una rama es independiente de la otra, debo salir del espacio; No puedo quedarme en el espacio. Como pueden ver, la matemática misma nos proporciona hechos que nos obligan a salir del espacio, si preservamos la continuidad de la idea. La realidad misma nos exige que en nuestras ideas salgamos del espacio. Incluso en Matemáticas, por lo tanto, nos enfrentamos a algo que nos muestra que, de alguna manera, debemos dejar el espacio atrás, si la idea pura es seguir el camino correcto. Teniendo la idea y comenzando a pensar en el proceso, debemos seguir pensando de tal manera que el espacio ya no nos sea de ninguna ayuda. Si esto no fuera así, no deberíamos poder calcular todas las posibilidades en la ecuación.

Al seguir una línea de pensamiento similar, nos encontramos con otras instancias de este tipo. Solo llamaré su atención al siguiente paso, lo que asegura si uno dice lo siguiente.  La elipse es el lugar de la suma constante —se define por el hecho de que es la curva de la suma constante. La hipérbola es la curva de diferencia constante. La curva de Cassini en sus diversas formas es la curva del producto constante. Debe haber también una curva de cociente constante, si tenemos aquí A, aquí B, aquí un punto M, y luego un cociente constante que se formará a través de la división de BM por AM. Debemos poder encontrar diferentes puntos, M 1, M 2, etc., para los cuales

etc. son iguales entre sí y siempre iguales a un número constante. Esta curva es, de hecho, el círculo. Si buscamos los puntos M1, M2, etc., encontramos un círculo que tiene esta relación particular con los puntos A y B (Fig. 8). Para que podamos decir: Además de la definición simple y habitual de un círculo, es decir, que es el lugar geométrico de un punto cuya distancia desde un punto fijo permanece constante, existe otra definición. El círculo es esa curva, cuyo punto cumple la condición de que sus distancias desde dos puntos fijos mantengan un cociente constante.

Ahora, al considerar el círculo de esta manera, hay algo más que observar. Para ver, si expresamos esto

(por supuesto, podría expresarse de alguna otra manera), siempre obtenemos los valores correspondientes en la ecuación y podemos encontrar el círculo. Al hacer esto, encontramos diferentes formas del círculo (es decir, diferentes proporciones entre el radio del círculo y la longitud de la línea recta AB), de acuerdo con la proporción de m a n. Estas diferentes formas del círculo se comportan de tal manera que su curvatura se vuelve cada vez menos. Cuando n es mucho mayor que m, encontramos un círculo con una curvatura muy fuerte; cuando n no es mucho mayor, la curvatura es menor. El círculo se hace más y más grande cuanto más pequeña es la diferencia entre n y m. Y si seguimos esta proporción de m hasta n aún más, el círculo pasa gradualmente a una línea recta. Puedes seguir esto en la ecuación. Se pasa al propio eje de ordenadas. El círculo se convierte en el eje de ordenadas cuando m = n, es decir, cuando el cociente m / n = 1. De esta manera, el círculo cambia gradualmente al eje de ordenadas, a una línea recta.

No es necesario que se sorprendan particularmente de esto. Es muy posible imaginarlo. Pero sucede algo muy diferente si deseamos seguir el proceso aún más. El círculo se ha aplanado más y más, y al volverse más plano desde el interior, por así decirlo, se transforma en una línea recta. Hace esto porque la razón constante en la ecuación sufre un cambio. A través de esto, el círculo se convierte en una línea recta. Pero esta relación constante puede, por supuesto, crecer más allá de 1, de modo que los arcos de los círculos aparecen aquí (a la izquierda del eje y). Sin embargo, ¿qué debemos hacer si tratamos de seguirlo en nuestra imaginación? Tenemos que hacer algo bastante peculiar. De hecho, tenemos que pensar en un círculo que no esté curvado hacia el interior, sino que esté curvado hacia el exterior. Por supuesto, no puedo dibujar este círculo, pero es posible pensar en un círculo que esté curvado hacia el exterior[1]. En un círculo ordinario, la curvatura es hacia el interior, ¿no es así?

Si seguimos la línea, regresa a sí misma. Pero definiendo el círculo de esta otra manera, si usamos la constante necesaria, obtenemos una línea recta. La curvatura todavía está en este lado (a la derecha del eje y). ¡Pero ahora hace que las cosas no sean tan cómodas para nosotros como antes! Anteriormente, la curvatura siempre giraba hacia el centro del círculo, mientras que ahora (en el caso de la línea recta), se nos muestra que el centro está en algún lugar en la distancia infinita, como se dice. A partir de esto, surge la idea de un círculo que se curva hacia el exterior. Su curvatura ya no es como está aquí (Fig. 9a), que sería el círculo filisteo común y corriente, pero su curvatura está aquí (Fig. 9b). Por lo tanto, el interior de este círculo no está aquí; este es el exterior; El interior de este círculo (Fig. 9c) está a la derecha.

Ahora comparen lo que acabo de poner delante. He descrito la curva de Cassini, con sus diversas formas, la lemniscata y la forma en que hay dos ramas. Y ahora hemos imaginado el círculo de tal manera que en un momento está curvado de la manera familiar, con el interior aquí y el exterior aquí; mientras que en una segunda forma de círculo (al dibujarlo solo indicamos lo que se quiere decir) encontramos que la curvatura es así, con un interior aquí y un exterior aquí. Comparándolo con la curva de Cassini, la primera forma del círculo correspondería a las formas cerradas, hasta la lemniscata. Después de esto tenemos otro tipo de círculo, que debe pensarse en la otra dirección, curvado de esta manera, con el interior aquí y el exterior aquí. Verán, cuando nos preocupamos por el producto constante, encontramos formas de la curva de Cassini donde, es cierto, nos arrojan fuera del espacio, pero aún podemos dibujar la otra rama en el otro lado. La otra rama está una vez más en el espacio, aunque para pasar de una a la otra nos expulsan del espacio. Aquí, en el caso del círculo, sin embargo, el asunto se vuelve aún más difícil. En la transición del círculo a la línea recta, de hecho, somos expulsados ​​del espacio y, además, ya no podemos dibujar una forma autónoma. Esto no podemos hacerlo. Al pasar de la curva del producto constante a la curva del cociente constante, solo podemos indicar el pensamiento espacialmente.

Es extraordinariamente importante que nos preocupemos por la creación de ideas que, por así decirlo, todavía se deslizarán en tales formas curvas. Estoy convencido de que la mayoría de las personas que se preocupan por las matemáticas toman nota de tales discontinuidades, pero luego hacen que el pensamiento sea más cómodo simplemente sosteniendo la fórmula y no pasando a lo que debería acompañar a la fórmula matemática en la verdadera continuidad del pensamiento. Tampoco he visto nunca que en el tratamiento de las Matemáticas como materia de educación se otorgue un gran valor a la formación de tales pensamientos en la imaginación —no lo sé— pregunto a los matemáticos presentes, Herr Blümel, Herr Baravalle, si es así; ¿En la educación universitaria moderna se le da alguna importancia? (El Dr. Unger mencionó aquí el uso del cine). Sí, pero eso es un pretexto. Solo es posible representar tales cosas dentro del espacio empírico por medio del cine o de manera similar, si se introduce algún tipo de engaño. No puede representarse completamente en el espacio real sin que el efecto se logre mediante alguna forma de engaño. El punto es, si hay algún lugar en la esfera de la realidad que nos obligue a pensar de manera realista en términos de tales curvas. Esta es la pregunta que estoy haciendo ahora. Sin embargo, antes de pasar a describir lo que tal vez corresponda a estas cosas en el ámbito de la realidad, me gustaría agregar algo que quizás pueda facilitarles la transición de estas ideas abstractas a la realidad. Es lo siguiente.

 

Pueden establecer otro problema en el ámbito de la astronomía teórica, la física teórica. Pueden decir: supongamos que aquí, como A, es una fuente de luz, y esta fuente de luz ilumina un punto M (Fig. 10). La fuerza de la luz que brilla desde M se observa desde B. Es decir, con los instrumentos ópticos necesarios, se observa desde B la fuerza de la luz que brilla desde el punto M, que se ilumina desde A. Y, por supuesto, en la intensidad de la luz variará de acuerdo con la distancia entre B y M. Pero hay un camino que podría describirse por el punto M, de modo que, al iluminarse desde A, siempre vuelve a B con la misma intensidad. Hay tal camino; y por lo tanto podemos preguntar: ¿Cuál debe ser el lugar geométrico de un punto, iluminado desde un punto fijo A, de modo que, visto desde otro punto fijo B, su luz sea siempre de la misma intensidad? ¡Esta curva —la curva en la cual tal punto tendría que moverse— es la curva de Cassini! De esto se ve que algo que adquiere una naturaleza cualitativa se establece en una conexión espacial, encajando en una curva complicada. La calidad que debemos ver en el haz de luz —porque la intensidad de la luz es una cualidad— depende en este caso del elemento de forma en las relaciones espaciales. Solo deseaba presentarles esto para que vean que hay al menos alguna forma de pasar de lo que se puede comprender en forma geométrica a lo cualitativo. Este camino es largo, y lo que discutiremos ahora es algo sobre lo que quiero llamar su atención, aunque tomaría meses presentarlo con todo detalle. Deben ser plenamente conscientes de que solo tengo la intención de darles las líneas guía; les corresponde a ustedes desarrollarlas más y entrar en todos los detalles que darían testimonio de la verdad de lo que se dice. Como pueden ver, la conexión que debe formarse entre la ciencia espiritual y las ciencias empíricas de hoy exige un trabajo extenso y de gran alcance. Pero cuando una vez se dan líneas de dirección, este trabajo puede en cierta medida llevarse a cabo y llevarse adelante. Es en todo caso posible. Uno solo debe ser capaz de penetrar de manera bastante definida en los fenómenos empíricos.

Si ahora abordamos el problema desde otro ángulo —hemos tratado de entenderlo en cierto grado desde el aspecto matemático, entonces, para cualquiera que esté estudiando el organismo humano, hay algo que no puede pasar desapercibido, algo que a menudo se ha presentado en nuestro círculo, especialmente en las conversaciones que acompañaron el curso de conferencias sobre medicina en Dornach en la primavera de 1920. No debe pasarse por alto que existen ciertas relaciones entre la organización de la cabeza y el resto de la organización humana, por ejemplo, el metabolismo. De hecho, hay una conexión, indefinible para empezar, entre lo que ocurre en el tercer sistema del ser humano —en todos los órganos del metabolismo — y lo que ocurre en la cabeza. La relación está ahí, pero es difícil de formular claramente a medida que emerge en varios fenómenos —por ejemplo, es obvio que ciertas enfermedades están relacionadas con deformidades del cráneo o la cabeza y similares, y estas cosas pueden ser fácilmente identificadas por alguien que intenta seguirlas con un razonamiento biológico— sin embargo, es difícil comprender esta relación en la imaginación. Las personas no suelen ir más allá del punto de decir que debe haber algún tipo de conexión entre lo que ocurre en la cabeza, por ejemplo, y en el resto del organismo humano. Es una imagen difícil de formar, solo porque es muy difícil para las personas hacer la transición del aspecto cuantitativo al cualitativo. Si no estamos educados a través de métodos científico-espirituales para encontrar esta transición, independientemente de lo que ofrece la experiencia externa —para extender a lo cualitativo el tipo de pensamiento que usamos para lo cuantitativo, si no nos entrenamos metódicamente para hacer esto, entonces, mis queridos amigos, siempre habrá un límite aparente para nuestra comprensión de los fenómenos externos.

Permítanme indicarles una forma en la que pueden entrenarse metodológicamente para pensar lo cualitativo de manera similar a como piensan lo cuantitativo. Todos ustedes están familiarizados con el fenómeno del espectro solar, el espectro continuo habitual. Saben que tenemos allí la transición del color del rojo al violeta. También saben que Goethe luchó con el problema de cómo este espectro es, en cierto sentido, lo contrario de lo que debe surgir si se permite que la oscuridad pase a través del prisma de la misma manera que se hace habitualmente con la luz. El resultado es una especie de espectro invertido y, como saben, Goethe también organizó este experimento. En el espectro ordinario, el verde pasa por un lado hacia el violeta y por el otro hacia el rojo; mientras que en el espectro obtenido por Goethe al aplicar una franja de oscuridad al prisma hay una flor de durazno en el medio y luego otra vez roja por un lado y violeta por el otro (Fig. 11). Se obtienen las dos bandas de color, cuyos centros son opuestos entre sí, cualitativamente opuestos, y ambas bandas parecen estirarse como si fueran al infinito. Pero ahora, uno puede imaginar que este eje, el eje longitudinal del espectro ordinario, no es simplemente una línea recta, sino un círculo, ya que de hecho cada línea recta es un círculo. Si esta línea recta es un círculo, regresa a sí misma, y ​​podemos considerar el punto donde la flor de durazno parece ser el mismo punto en el que el violeta, que se extiende hacia la derecha, se encuentra con el rojo, que se extiende hasta la izquierda. Se encuentran en la distancia infinita a derecha e izquierda. Si tuviéramos éxito —tal vez sepan que uno de los primeros experimentos que se realizarán en nuestro laboratorio físico recientemente establecido es estar en esta dirección— si tuviéramos éxito en doblar el espectro de cierta manera en sí mismo, entonces incluso aquellos que no están dispuestos a comprender el asunto para empezar, en el pensamiento puro seremos capaces de ver que aquí estamos interesados ​​en algo real y de naturaleza cualitativa.

 

 

Llegamos a ciertas ideas limitantes en Matemáticas, donde —como en Geometría sintética—  estamos obligados a considerar la línea recta como un círculo en un sentido bastante real aunque interno; donde estamos obligados a admitir que el punto infinitamente distante de una línea recta es solo un punto; o entender como delimitar un plano, no una línea arriba y luego otra vez abajo, sino una sola línea recta; o pensar en el límite del espacio infinito, no en la naturaleza de algo esférico, sino como un plano. Sin embargo, tales ideas también se convierten, en cierto modo, en ideas limitantes para la realidad empírica perceptible por los sentidos, y estamos hechos para darnos cuenta si insistimos en restringirnos a la realidad perceptible por los sentidos.

Esto nos lleva a algo que de otro modo siempre permanecería perpetuamente en la oscuridad. Ya lo he mencionado. Realmente nos invita a reflexionar sobre las imágenes de pensamiento a las que llegamos cuando permitimos que la forma de lemniscata de la curva de Cassini pase a la forma de doble ramificación —la forma con las dos ramas para las cuales debemos salir del espacio—  y ellos comparan esto con lo que nos enfrenta en la realidad empírica.

De hecho, ya están haciendo esto, mis queridos amigos, cuando aplican las Matemáticas de una forma u otra a la realidad empírica. Llaman a un triángulo «triángulo», porque primero lo han construido matemáticamente. Aplican a la forma externa lo que ha evolucionado de manera constructiva dentro de ustedes. El proceso que acabo de describir es más complicado, pero es el mismo proceso cuando piensan en las dos ramas de esa forma particular de la curva de Cassini como una sola. Aplican este pensamiento a la correspondencia entre la cabeza humana y el resto del organismo humano y tendrán que darse cuenta de que en la cabeza hay una conexión con el organismo restante de un carácter tal como lo expresa la ecuación que requiere, no una curva continua, sino discontinua. Esto no puede seguirse anatómicamente; deben ir más allá de lo que el cuerpo comprende físicamente, si encuentran la conexión de lo que se expresa en la cabeza con lo que se expresa en el sistema metabólico. Es esencial acercarse al organismo humano con pensamientos que son bastante inalcanzables si por cada elemento del pensamiento insisten en una correspondencia completa dentro del ámbito empírico perceptible por los sentidos. Debemos alcanzar algo más, más allá del ámbito empírico perceptible por los sentidos, si queremos encontrar cuál es realmente esta relación dentro del ser humano.

Tal estudio, si uno realmente se entrega y lo realiza metódicamente, es extraordinariamente rico en sus resultados. La organización humana es de tal naturaleza que no puede ser adoptada solo por el enfoque anatómico. Así como somos expulsados ​​del espacio en la curva de Cassini, en el estudio del hombre somos expulsados ​​del cuerpo, por el método de estudio mismo. Como puede ver, es muy posible comprender, en primer lugar, en el pensamiento, que en un estudio del hombre en su totalidad somos expulsados ​​del ámbito de lo que puede captarse en un sentido físico-empírico. Presentar tales cosas no es una ofensa contra los principios científicos. Tales ideas están muy alejadas de las fantasías puramente hipotéticas que a menudo se entretienen en relación con los fenómenos naturales, ya que se refieren a la forma total en que el hombre se integra en el universo. No estás buscando algo que de otro modo no existiría, sino algo que es exactamente igual a lo que se expresa en la relación entre un hombre que piensa matemáticamente y la realidad empírica.

No se trata de buscar hipótesis que al final sean injustificables; es una cuestión, dado que la realidad es obviamente complicada, de buscar otras relaciones cognitivas con la realidad interna, además de la simple relación del hombre matemático con la realidad empírica. Cuando una vez que hayan aceptado tales pensamientos, también se les preguntará si lo que ocurre fuera del ser humano en otros dominios además del astronómico —por ejemplo, en aquellos fenómenos que llamamos químicos y físicos— si esos mismos fenómenos, que consideramos fenómenos químicos fuera del hombre, siguen el mismo curso dentro del hombre, cuando está vivo, como lo hacen fuera de él, o si aquí también es necesaria una transición que conduzca de alguna manera al espacio.

Ahora consideren la importante pregunta que surge de esto. Supongamos que tenemos aquí algún tipo de fenómeno químico y aquí el límite que conduce al interior del ser humano (Fig. 13). Suponiendo que este fenómeno químico fuera capaz de provocar otro, de modo que el ser humano reaccionara aquí (adentro); entonces, si permanecemos en el campo de lo empírico, el espacio sería, por supuesto, el mediador. Sin embargo, si la continuidad de este fenómeno dentro del ser humano se produce en virtud del hecho, digamos, de que el ser humano se nutre de alimentos y los procesos que ya tienen lugar fuera de él continúan dentro de él, entonces surge la pregunta: ¿La fuerza que actúa en el proceso químico permanece en el mismo espacio cuando tiene lugar dentro del hombre que cuando sigue su curso fuera de él? ¿O tal vez debemos salir del espacio?

Y ahí tienes lo que es análogo al círculo que se transforma en una línea recta. Si buscan su otra forma, donde lo que generalmente se gira hacia afuera ahora se vuelve hacia adentro, están completamente fuera del espacio.

 

La pregunta es si no necesitamos ideas como estas, imágenes de pensamiento que, si bien son continuas, salen directamente del espacio, cuando seguimos el curso de lo que sucede externamente, fuera del hombre, hacia el interior del ser humano. Lo único que se puede decir contra tales cosas, mis queridos amigos, es que ciertamente imponen mayores exigencias a la capacidad humana de comprensión que las ideas con las que se abordan los fenómenos de hoy. Por lo tanto, podrían ser bastante incómodas en la educación universitaria. Son, sin duda, completamente incómodas, porque implican que antes de acercarnos a los fenómenos debemos despertar en nosotros mismos lo que nos permitirá comprenderlos. Nada de esto existe en nuestro sistema educativo actual; pero debe venir, ciertamente debe venir, de lo contrario, simplemente hablando de un fenómeno nos encontramos con las mayores disparidades, sin ver de ninguna manera la realidad. Solo piensen qué sucede cuando alguien observa el círculo mientras se curva hacia este lado (Fig. 9a), y luego ven cómo se curva hacia este lado (Fig. 9b), pero luego permanecen filisteos y simplemente no conciben que el círculo ahora curve hacia el otro lado. Él dice: Esto es imposible, el círculo no puede curvarse de esta manera; Debo poner la curvatura de esta manera, simplemente debo colocarme del otro lado. De lo que está hablando parece ser una misma cosa; pero ha cambiado su punto de vista.

De esta manera, hoy simplificamos las cosas al describir lo que está dentro del ser humano en comparación con lo que ocurre en la Naturaleza fuera de él. Decimos: lo que hay dentro del hombre no existe en absoluto; Simplemente debo ubicarme dentro del hombre y decir que la curvatura está orientada de esta manera (Fig.9c). Luego consideraré lo que hay dentro, sin tener en cuenta que he invertido la curvatura. Convertiré el interior del ser humano en una Naturaleza externa. Simplemente imagino que la naturaleza exterior continuará a través de la piel hacia el interior. Me doy la vuelta, porque no estoy dispuesto a admitir la otra forma de curvatura, y luego teorizo. Ese es el truco que se realiza hoy, solo para adherirse a movimientos más cómodos. No hay deseo de acentuar lo que es real; para no tener que hacerlo, simplemente nos damos la vuelta y, esto es ahora una comparación, en lugar de mirar al humano desde el frente, miramos a la Naturaleza desde atrás y llegamos de esta manera a todas las diversas teorías sobre el hombre

Continuaremos, entonces, mañana.

 

Traducción revisada por Gracia Muñoz en octubre de 2019

 

 

 

[1] Si se dibujara, se vería como un círculo ordinario, solo uno tendría que tener en cuenta que «afuera» y «adentro» habían cambiado de lugar. (Nota del editor.)