Del ciclo: «La relación de las diversas ramas de las ciencias naturales con la astronomía»

Rudolf Steiner — Stuttgart, 15 de enero de 1921

Versión en ingles

Mis queridos amigos,

Hoy me ocuparé de algunas de las cosas que pueden estar causando dificultades para comprender lo que hemos hecho hasta ahora. Pasaré de estas dificultades a un reino de ideas que mostrarán la insuficiencia de esas líneas de pensamiento en las que la gente de nuestro tiempo, con todos sus cómodos hábitos mentales, encontraría gustosamente su comprensión de los fenómenos universales.

Hemos estado estudiando los fenómenos universales en su relación con el hombre. Lo hemos hecho en múltiples direcciones. Una y otra vez hemos indicado cómo se revela una relación entre la formación del hombre y lo que aparece en los fenómenos celestes. Ya sea que nos guiemos por algún sistema cósmico antiguo o por las teorías copernicanas al formar nuestra síntesis pictórica de los movimientos de los cuerpos celestes, debemos relacionar la imagen con el hombre de diversas maneras, por supuesto, en consecuencia. Esto lo hemos visto. Para una verdadera ciencia debemos aceptar que existe esta relación.

Sin embargo, las dificultades son formidables. Anteriormente en estas conferencias llamamos la atención sobre una de esas dificultades. En el momento en que intentamos formar relaciones entre los períodos de revolución de los planetas de nuestro sistema, llegamos a números inconmensurables. La aritmética se agota, como podríamos decir; no llegamos más lejos con él, porque donde entran números inconmensurables no hay unidad palpable. Así, cuando buscamos una síntesis de los fenómenos del espacio cósmico con nuestro método matemático y forma de pensar habituales, los fenómenos en sí mismos son tales que nos encontramos cada vez más alejados de la realidad. Por tanto, no podemos dar por sentado que alguna vez seremos capaces de explicar los fenómenos cósmicos sobre la base acostumbrada de nuestra Geometría, es decir, dentro de un espacio rígido tridimensional. Es más, ha surgido otra dificultad. Ayer nos vimos obligados a asumir una cierta relación entre el Sol, la Luna y la Tierra, encontrando expresión de alguna manera en el hombre, en la estructura misma del hombre. De buena gana comprenderíamos cómo es la relación. Sin embargo, si postulamos este trabajo conjunto de los Tres, nos metemos en formidables dificultades en el cálculo espacial.

Todas estas cosas las hemos mencionado. Ahora podemos llegar a un cierto punto de partida al menos, a través de la geometría pura —una geometría sin embargo de un tipo superior. De ahí podemos tener una idea de dónde vienen las dificultades cuando intentamos, a fuerza de cálculo espacial, captar la interconexión de los fenómenos celestes. Recordemos nuestros preciosos intentos de comprender la forma del hombre mismo. Entonces se nos permite esto: —Podemos y debemos tratar de tomar en serio esa ‘pertenencia’ al ser humano de la que también hemos hablado en estas conferencias. La organización de la cabeza humana, podemos decir verdaderamente, centrada como esta en el sistema nervioso y perceptivo, es relativamente independiente. También lo es el sistema rítmico con todo lo que le pertenece. El sistema metabólico también, y en todo lo que lo acompaña en la organización, se revelan tres sistemas independientes. Partiendo ahora de forma inteligente desde el principio de la metamorfosis, como siempre debemos hacer cuando se trata de la Naturaleza orgánica, podemos intentar formarnos ideas sobre esta cuestión: ¿Cómo se relacionan los tres miembros del triple sistema humano con cada uno, según este principio de metamorfosis?

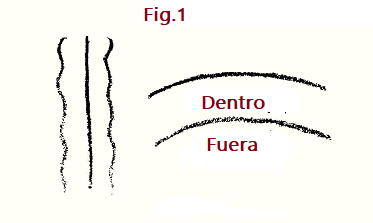
Entiéndame bien, mis queridos amigos. Queremos tener una idea, aunque sea sólo pictórica para empezar, de cómo los tres miembros del sistema humano se relacionan entre sí. A primera vista, por supuesto, será difícil. En los órganos que se encuentran en la cabeza humana, será difícil reconocer claramente en ellos la metamorfosis de aquellos órganos que son fundamentales para el sistema metabólico y linfático. Pero si nos adentramos lo suficiente en la morfología del hombre, podremos encontrar nuestro camino. Solo tenemos que pensar más a fondo en las líneas ya indicadas. Es decir, la esencia de la relación mutua del hueso largo con el hueso del cráneo y viceversa es un giro completo de adentro hacia afuera. La superficie interna del hueso se convierte en la vuelta hacia afuera. Es el principio por el cual se gira un guante de adentro hacia afuera, siempre que el giro de adentro hacia afuera implique un cambio simultáneo en las relaciones inherentes de las fuerzas internas. Si volviera un hueso tubular o un hueso largo de adentro hacia afuera como un simple guante, volvería a tener la forma de un hueso tubular, no hace falta decirlo. Pero no será así si partimos, como debemos hacer, de la configuración inherente del hueso. Como describí antes, en su configuración inherente, el hueso largo está orientado hacia adentro, hacia la cualidad radial que lo atraviesa. Por tanto, está obligado a someter su estructura material y su disposición al principio radial. Cuando lo haya «volteado», de modo que el lado interior se abra hacia fuera, en su configuración ya no seguirá el principio radial sino el esferoidal. El «lado interno», ahora vuelto hacia afuera hacia la Esfera, recibirá esta forma (Fig. 1).

Lo que antes estaba afuera, ahora está adentro y viceversa. Tengan esto en cuenta para la metamorfosis extrema del hueso tubular en hueso del cráneo y dirán: Los extremos más externos de la membresía humana —sistema linfático y sistema craneal— representan polos opuestos en la organización del hombre. Pero no debemos pensar en «polos opuestos» en el mero sentido trivial y lineal de la palabra. Al ir de un polo al otro, debemos adoptar la transición que esto implica, es decir, del Radio a la superficie de una Esfera. Sin la ayuda de tales ideas e imágenes mentales, por intrincadas que parezcan, es imposible obtener una noción justa o adecuada de lo que es el cuerpo humano.

Llegamos ahora a lo que constituye el medio, en cierto sentido, el miembro medio de la organización del hombre. Esto es todo lo que pertenece al sistema rítmico, y de alguna manera formará la transición de la estructura radial a la esferoidal. En el sistema triple así presentado tenemos la clave para la comprensión morfológica de todo el organismo humano. Por supuesto, debemos darnos cuenta de cómo será. Supongamos que tenemos algún órgano en el sistema metabólico —el hígado, por ejemplo— o cualquiera de los órganos asignados principalmente al metabolismo. (Debemos calificarlo con la palabra ‘principalmente’ porque siempre hay una superposición y un entrelazamiento de estas cosas). Supongamos entonces que comenzamos con un órgano así y buscamos las respuestas en la cabeza. Tratamos de encontrar cuál de los órganos de la naturaleza de la cabeza del hombre puede estar conectado con él por la metamorfosis de dar la vuelta al revés. Entonces tendremos que reconocer el órgano cuando está completamente transformado, deformado; sólo así lo entenderemos. Por tanto, no será fácil de asimilar matemáticamente. Sin embargo, sin encontrar alguna forma matemática de acceso, nunca la captaremos adecuadamente. Y si lo recuerdan (aunque solo tomen esto como una imagen) —si recuerdan que la comprensión real de la forma y la figura humanas nos conducirá entre los movimientos de los cuerpos celestes, adivinarán lo que debe ser necesario también cuando deseemos comprender este último. Para una verdadera síntesis de los fenómenos de movimiento entre los cuerpos celestes, será bastante inadecuado pensar en ellos como si estos movimientos fueran accesibles a una Geometría que simplemente tiene en cuenta el espacio rígido ordinario y, por lo tanto, no puede dominar el giro de adentro hacia afuera. Porque cuando hablamos de un giro de adentro hacia afuera en la forma en que lo hemos estado haciendo, ya no podemos estar pensando en el espacio ordinario. El espacio ordinario es válido donde podemos calcular los volúmenes, el contenido del cubículo de la manera convencional. No podemos hacerlo si nos vemos obligados a hacer el interior exterior. Ya no podemos seguir calculándolos con las mismas concepciones que se mantienen en el espacio ordinario.

Entonces, si al pensar en la forma y figura humanas necesito los giros de adentro hacia afuera, al pensar en los movimientos de los cuerpos celestes, los necesitaré también. No puedo proceder como la Astronomía actual que trata de comprender los fenómenos celestes dentro de una forma rígida ordinaria de espacio.

Tomemos, para empezar, simplemente la organización cefálica y la organización metabólica del hombre. Para pasar de uno a otro hay que imaginar, una vez más, un giro de adentro hacia afuera —y, además, uno que implica variaciones de forma. Intentemos al menos hacernos una idea del tipo de pensamiento involucrado. Hicimos un trabajo preliminar en esta dirección cuando hablamos de las curvas de Cassini y del círculo concebido de manera diferente. Por lo general, el círculo se define como una curva, cuyos puntos son equidistantes de un punto central. Estábamos hablando del círculo como una curva, cuyos puntos están a distancias medidas de dos puntos fijos, de modo que el cociente de las dos distancias es constante. Esta fue nuestra otra concepción del círculo.

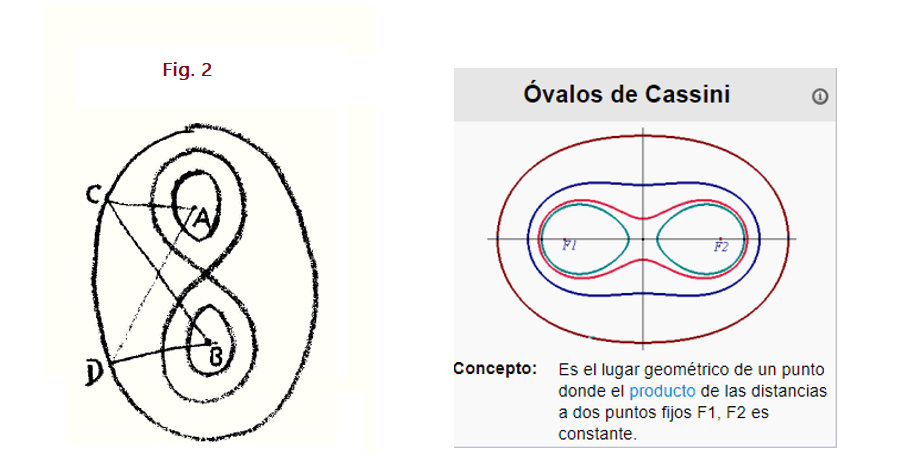
Hablando de la curva de Cassini, mostramos que tiene tres formas esenciales. Una, no muy diferente a una elipse: —esta forma surgió cuando los parámetros de la curva tenían una cierta relación, la que indicamos. La segunda forma fue la lemniscata. La tercera forma es que mientras en la idea de ella —y también analíticamente— es una entidad única, al mirarla no lo es. Tiene dos ramas (Fig. 2), pero las dos ramas son una curva. Para trazar la línea, de alguna manera deberíamos tener que salir del espacio, volviendo al espacio nuevamente cuando dibujamos la segunda rama. Conceptualmente, nuestra mano estaría dibujando una línea continua al dibujar las dos regiones que parecen separadas. No podemos trazar la línea continuamente dentro del espacio ordinario y, sin embargo, conceptualmente, lo que está aquí arriba y lo que está aquí abajo (la curva interior en la Figura 2) es una sola línea. Ahora, como también mencioné, la misma curva se puede pensar de otra manera. Puedes preguntar cuál será la trayectoria de un punto que cuando se ilumina desde un punto fijo A aparece con intensidad constante de iluminación, visto desde otro punto fijo B. Respuesta: una curva de Cassini. Una curva a Cassini será el foco de todos los puntos a través de los cuales debe pasar un punto, si cuando se ilumina desde un punto fijo A se ve alguna vez con la misma intensidad de luz desde otro punto fijo B (Fig. 2 nuevamente).

Ahora bien, no les resultará difícil imaginar que si algo brilla de A a C (Fig. 2) y de allí por reflexión de C a B, la intensidad de la luz será la misma que si se reflejara en D en su lugar. Pero se vuelve bastante más difícil de imaginar cuando vienes a la Lemniscata. Las construcciones geométricas ordinarias por las leyes de la reflexión y demás, no serán tan fáciles de llevar a cabo. Y se vuelve aún más difícil imaginar con la curva de dos ramificaciones, que la misma intensidad de luz debería observarse siempre desde el punto B, dentro de la única ramificación de la curva, cuando la fuente puntual de luz original está en A. Tendrías que imaginar (al pasar de una rama a la otra) que el rayo de luz sale del espacio y luego vuelve a brillar en el espacio. Te enfrentas a la misma dificultad que antes, cuando simplemente se te pidió que dibujaras las dos ramas como una —con un solo movimiento de la mano a través del espacio.

Sin embargo, si no desarrollamos estos conceptos seremos desiguales para la otra tarea, a saber, encontrar la transmutación —o incluso la mera relación de forma— como entre cualquier órgano en la cabeza del hombre y el órgano correspondiente en el metabolismo. Para encontrar la conexión, simplemente deben salir del espacio. Una vez más —por extraño que parezca— si con su comprensión de cualquier forma en la cabeza humana desean hacer una transición hacia la comprensión de una forma en el sistema metabólico humano, entonces no podrán permanecer en el espacio. Deben salir del espacio. Debes salir de ti mismo, buscando algo que no está en el espacio. Encontrarán algo tan pequeño dentro del espacio ordinario como lo que interviene entre las ramas superior e inferior de una curva de Cassini de dos ramas. Ésta es, de hecho, sólo otra forma de expresar lo dicho antes de que la metamorfosis debe ser concebida de tal modo que la forma se dé la vuelta completamente.

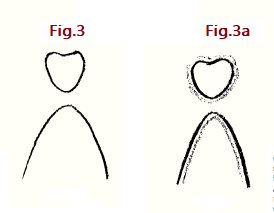
Al pensar así en la conexión entre las ramas superior e inferior de la curva discontinua de Cassini (como se muestra en la Fig. 3), todavía estamos presuponiendo constantes reales, rígidas y sin cambios, en la ecuación. Ahora bien, si variamos las constantes en sí mismas como en una lección anterior, formando ecuaciones de variabilidad doble, podremos imaginar la rama superior, digamos, en esta forma y la inferior en esta (Fig. 3).

La rama superior tomará esta forma eventualmente. Si entonces altera la curva de Cassini tomando variables en lugar de constantes —para comenzar con ecuaciones en lugar de con constantes invariables— obtendrá dos tipos diferentes de ramas. Entonces también existirá la posibilidad de que una de las dos ramas entre por así decirlo desde el infinito y vuelva a salir al infinito. Esta es precisamente la relación a partir de la cual debes partir al seguir ciertas formas dentro de la cabeza humana, que las comprenden en curvas y líneas, y luego relacionarlos con las formas de órganos o de complejos de órganos en el sistema metabólico, que a su vez estará integrado en curvas y líneas. Tal es la complejidad de la forma humana. Para hacerlo aún menos simple, deben imaginar una línea (Fig. 3a) con una tendencia hacia afuera y la otra con su tendencia hacia adentro.

Serán propensos a decir (espero sin insistir, pero como una impresión pasajera): Si esto es así, la organización humana es tan complicada que uno casi preferiría prescindir de tal comprensión y recurrir a la idea filistea ordinaria del cuerpo, como en la Anatomía y Fisiología actuales. ¡Allí no se nos pide que hagamos esfuerzos tan prodigiosos como para dejar que las imágenes mentales se desvanezcan y, una vez más, no desaparezcan, o ponerlas del revés, y todo lo demás! Tal vez; pero entonces nunca comprenderás realmente la forma humana; tu comprensión es, a lo sumo, ilusoria.

Ahora, para continuar: supongamos que lo miras y reconoces que hay algo en la organización humana que cae directamente del espacio, que no está en el espacio en absoluto, pero que te obliga, por ejemplo, a imaginar sistemas lineales separados espacialmente, inherentemente. unidos entre sí y, sin embargo, unidos por otro principio que el que ofrece el espacio tridimensional. Pensando de esta manera, ya no se alejará demasiado de lo que ahora voy a presentar. Al menos podrán entretener el pensamiento en un sentido formal. Nadie, quiero decir, puede objetar válidamente pensarlo como una forma pura de pensamiento. Para empezar, todo lo que estamos llamados a hacer es concebir una idea clara, como en las matemáticas en general. No se puede objetar que la cosa no esté probada o algo parecido. Solo nos preocupa llegar a una idea autónoma y coherente.

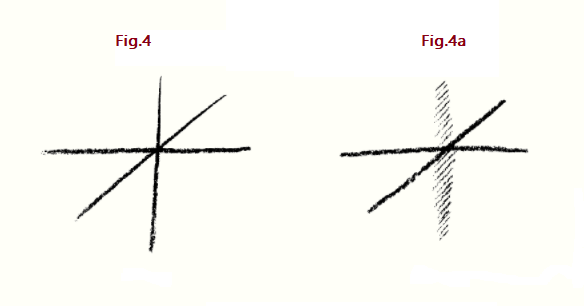
Piensen, pues, por un momento, que tendrán que ver no sólo con el espacio ordinario, concebido en sus tres dimensiones, sino con un «contraespacio» o «antiespacio». Déjenme llamarlo así por el momento, y trataré evocar una idea de ello, como sigue: Supongamos que formo el pensamiento de espacio ordinario, tridimensional, rígido. Formo la primera dimensión, formo la segunda dimensión y formo la tercera dimensión (Fig. 4).

Entonces he, por así decirlo, llenado de pensamientos —en la idea y presentación mental de la misma— el espacio tridimensional con el que normalmente me enfrento. Ahora, como saben, en cualquiera de esos dominios no sólo pueden avanzar hasta cierto grado de intensidad; también puede restar de él, y a medida que continúan restando —quitando— llegas por fin a la negación de ti. Como bien saben, no solo hay riquezas sino también deudas. Del mismo modo, no sólo puedo hacer que surjan las tres dimensiones en el pensamiento, sino que también puedo hacerlas desaparecer. Solo que ahora imagino el surgimiento y la desaparición como un proceso real, —algo realmente está ahí. Por supuesto, es posible pensar solo en dos dimensiones en lugar de tres, pero ese no es mi significado. Lo que quiero decir ahora es esto: la razón por la que solo tengo dos dimensiones (Fig. 4a) No es que nunca haya tenido una tercera. La razón es que tenía una tercera y se ha desvanecido. Las dos dimensiones son el resultado del surgimiento y la desaparición de la tercera. Ahora tengo un espacio que, aunque exteriormente muestra sólo dos dimensiones, debe concebirse interiormente como si tuviera dos terceras dimensiones, una positiva y la otra negativa. La dimensión negativa surge de una fuente que ya no puede estar allí en mi espacio tridimensional. Tampoco debo pensar en ella como una «cuarta dimensión» en el sentido convencional. No, debo pensar que es, en la tercera dimensión, de positivo a negativo (Fig. 4a una vez más).

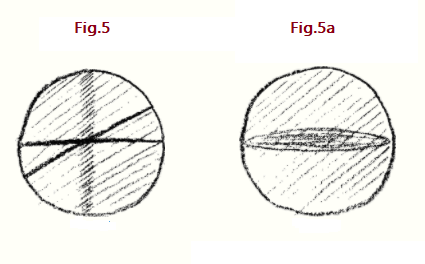
Y ahora supongamos que lo que he estado indicando está realmente en el Universo; sin embargo, como son las cosas generalmente en el mundo real, aproximadamente. Entonces no sería una interpretación pedantemicamente precisa sino aproximada de lo que he dibujado aquí. Esto no tiene por qué causarles ninguna gran sorpresa, porque en la realidad exterior perceptible por los sentidos nunca encuentras figuras matemáticas reproducidas de otra manera, siempre aproximadamente. Si entonces afirmo que la imagen representa algo real, solo esperaré que lo haga en un sentido aproximado. Para representar una realidad que le corresponda, no necesito repetir exactamente el mismo dibujo, pero debería dibujar algo aplanado; eso respondería a eso. El hecho de que algo haya estado allí y luego se haya desvanecido, quizás pueda sugerirlo de esta manera: supongo que la densidad de un efecto, indicada por el sombreado oscuro, surgió y luego se desvaneció parcialmente, se debilitó (Fig.5).

Luego te queda una esfera que tiene una porción más densa en la región media. Les ruego que sepan, comparen lo que se dibuja aquí con el sistema cósmico real, tal como lo vemos con nuestros ojos, la esfera cósmica con todas las estrellas ampliamente dispersas, y luego las estrellas más densamente empaquetadas en la región de la Vía Láctea, o lo que llamamos el Sistema Galáctico. Sin embargo, también puede compararlo con otra cosa. Tomen cualquier mapa estelar popular. La imagen que hemos mostrado (Fig.5a) —tomémoslo simplemente como una imagen—  es fundamentalmente equivalente a lo que siempre se muestra: el paso del Sol o de la Tierra por el Zodíaco, con los polos norte y sur de la eclíptica en algún lugar más allá. La idea que nos hemos estado formando, como ven, no está muy alejada de lo que hay en el Universo exterior. En las siguientes conferencias, por supuesto, todavía tendremos que buscar relaciones más detalladas.

Ahora, para comprender lo que se dijo antes sobre el ser humano, todavía no nos hemos acercado lo suficiente. Debemos ir más lejos y hacer que la segunda dimensión también se desvanezca; entonces nos quedaremos con solo una —con una línea recta. Pero esta no es una línea recta ordinaria dibujada en un espacio tridimensional. Es la línea que ha quedado cuando hemos hecho desaparecer la tercera y también la segunda dimensión. Y ahora hacemos que el último restante desaparezca. Entonces nos quedamos con un mero punto. Sin embargo, tengan en cuenta que hemos llegado a este punto mediante la desaparición sucesiva de tres dimensiones. Ahora supongamos que este punto se nos presentara en realidad, —como teniendo existencia en sí mismo. Si está allí y se hace sentir, ¿cómo imaginaremos su actividad? No podemos relacionar su actividad con ningún punto del espacio determinado por el eje x. El eje x no está ahí, ya que ha desaparecido. Tampoco podemos relacionarlo con nada con una x —y una coordenada y, porque todo esto se ha ido; todo esto ha desaparecido del espacio. Tampoco podemos relacionarlo en su actividad con la tercera dimensión del espacio. Entonces, ¿qué diremos? Cuando revele su actividad tendremos que relacionarlo con lo que está bastante fuera del espacio tridimensional. De acuerdo con el procedimiento por el que hemos pasado en nuestro pensamiento, no es posible que podamos relacionarlo con nada que todavía pueda incluirse en este espacio. Solo podemos relacionarlo con lo que está fuera de su espacio tridimensional por completo. No podemos relacionarlo ni con «x eliminado» ni con «y eliminado» ni con «z eliminado», sino solo con lo que elimina los tres, z, y, z juntos, y por lo tanto está dentro absolutamente del espacio tridimensional.

Para empezar, planteamos esto como una noción matemática puramente formal. Sin embargo, pronto se vuelve real. Se vuelve extremadamente real cuando empezamos a adentrarnos en las cosas más profundamente que con las nociones fáciles con las que la ciencia hoy en día las dominaría gustosamente. Miren, con esta tendencia más profunda de comprensión —observar el proceso de la vista y toda la organización del ojo. Quizás sepan (en otras conferencias de las que he hablado a menudo) de que el ojo no debe considerarse simplemente como una cosa formada desde dentro del cuerpo hacia afuera; porque está organizado en gran parte en el cuerpo desde fuera. Pueden rastrear su formación desde afuera hacia adentro al estudiar el desarrollo filogenético de los animales inferiores y luego considerar el acto de la vista en sí. Se las ingeniarán para comprender cómo se estimula el proceso de la vista desde fuera y cómo el órgano también se adapta a esta estimulación desde fuera. Luego, a medida que el proceso avanza hacia el interior del nervio óptico y más adentro, desaparece por fin, —desaparece por así decirlo en la organización en su conjunto. Sé que pueden encontrar la terminación de los nervios ópticos y, sin embargo, —esto también llega a expresarse aproximadamente— si te adentras en la organización interna, tendrás que admitir que allí desaparece.

Demasiado para el proceso de la vista y los órganos asociados. Y ahora comparen con esto el proceso de secreción de los riñones. Entren en ello concienzudamente. y tendrán que relacionar el conducto que conduce hacia el exterior, para la secreción de los riñones, con el que trabaja de afuera hacia adentro por donde el ojo pasa al nervio óptico. Si luego busca ideas mediante las cuales las dos cosas puedan relacionarse, de modo que su relación mutua les ayude a comprender los fenómenos de cualquiera de los procesos, encontrarán indispensables las formas de pensamiento que acabamos de indicar. Si conciben las ideas del espacio tridimensional como aplicadas al proceso de la vista (también podríamos reemplazar una por otra, pero si lo hacen de esta manera …), entonces, si buscan qué respuestas en la secreción de los riñones, deben darse cuenta de que lo que allí está representado te saca directamente del espacio tridimensional. Deben seguir el mismo procedimiento en su pensamiento que yo he hecho ahora para extinguir las dimensiones espaciales. De lo contrario, no encontrarán el camino.

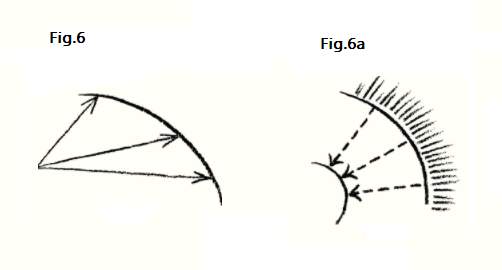
De la misma manera deben proceder si están tratando de entender las curvas formadas en los Cielos por los caminos aparentes de Venus y Mercurio, por un lado, Júpiter y Marte por el otro, me refiero simplemente a los caminos aparentes como los observamos con nuestros ojos, —incluidos los bucles. Si usan coordenadas polares, por ejemplo, entonces para el bucle de Venus puede hacer el origen de su sistema de coordenadas en un espacio tridimensional. Aquí pueden hacerlo. Pero no aceptarán la realidad si adopta el mismo principio al examinar la curva de Marte. En este caso, debe partir de la premisa ideal de que los orígenes de cualquier sistema relevante de coordenadas polares estarán fuera del espacio tridimensional. Están obligados a tomar las coordenadas de esta manera. En el primer caso, puede comenzar desde el polo del sistema de coordenadas, tomando las coordenadas de la forma normal, como en la Figura 6.

Pero si haces esto para la única curva planetaria —digamos por el camino de Venus con su bucle— harás igual justicia a los caminos de Júpiter o Marte con sus bucles, solo diciéndote a ti mismo: Esta vez no supondré un sistema de coordenadas polares con un origen tal que siempre tengo que agregar una pieza para obtener las coordenadas polares, como en la Figura 6. No, tomaré como origen de mi sistema de coordenadas polares la Esfera circundante (Figura 6a), es decir, lo que hay detrás de él, indeterminadamente lejos. Luego obtengo coordenadas como estas (líneas de puntos), donde en cada caso, en lugar de agregar, debo dejar muchas cosas fuera. La curva que obtengo también tiene algo así como un centro, pero el centro está en la esfera infinita.

Podría resultar necesario entonces, para una investigación más profunda de las trayectorias de los planetas, que hagamos uso de esta idea: al constituir las trayectorias de los planetas interiores debemos atribuir a estas trayectorias algún centro u otro dentro del espacio ordinario. Pero si queremos pensar en centros para el camino de Júpiter, el camino de Marte, etc., debemos ir directamente fuera de este espacio ordinario.

En fin, tenemos que superar el espacio; debemos trascenderlo. No hay ayuda para eso. Si eres consciente en tus esfuerzos por comprender los fenómenos, las meras ideas del espacio tridimensional no te bastarán. Debes imaginar la interacción de dos tipos de espacio. Uno de ellos, con las tres dimensiones ordinarias, puede concebirse como saliendo radialmente de un punto central. El otro, que todo el tiempo anula y extingue al primero, no puede pensarse en absoluto como que emana de un punto. Debe pensarse que procede de la Esfera circundante —es decir, la Esfera infinitamente lejana. Mientras que en el primer caso el «punto» tiene áreas cero que gira hacia afuera y un punto con el área de una superficie esférica infinita que gira hacia adentro. Geométricamente, puede bastar con concebir la noción de punto de manera abstracta. En el ámbito de la realidad no lo será. No haremos justicia a la realidad con la mera noción de un punto abstracto. En todos los casos debemos preguntarnos si el punto que estamos concibiendo tiene su curvatura hacia adentro o hacia afuera; su campo de influencia estará de acuerdo con esto.

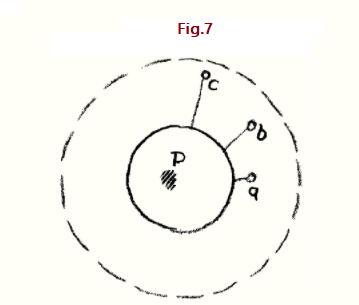
Pero debéis pensar aún más, mis queridos amigos; hay otra cosa. Por supuesto, pueden imaginar que en algún lugar captaron este punto que en realidad es una Esfera. Para empezar, dado que está en los infinitos espacios lejanos, no es necesario que lo imagines aquí (s, Fig. 7). También pueden imaginarlo un poco más lejos (b, o c). Pueden imaginarlo en cualquier lugar; solo tienen que dejar esta esfera libre (esfera fuertemente dibujada en la Fig. 7).

Porque esto está ahuecado, por así decirlo; este es el círculo invertido o la esfera invertida, si lo desean. Pero ahora suponga que lo siguiente podría ser el caso. Piense en lo que hay dentro de este círculo peculiar (es decir, en a, b, c, etc.) Piensen en este punto que tiene su curvatura hacia adentro. Porque, en efecto, todo el espacio fuera de esta superficie esférica es entonces un punto con su curvatura hacia adentro. Y ahora imagina que este espacio tenía, después de todo, su límite en alguna parte. Es posible que pueda ir muy lejos, muy lejos. Sin embargo, supongamos que la realidad fuera tal que no pudieras ir a cualquier parte, sino que, en algún lugar, después de todo, hubiera un límite de otro tipo (círculo de puntos en la Figura 7). Lo que allí parecería, como por necesidad interior, lo que en efecto pertenece al reino más allá del límite. Tendría que surgir una esfera equivalente en el interior, perteneciente a lo que hay fuera. Entonces tendrías que darte cuenta: allá afuera, más allá de una determinada esfera, algo todavía existe, es cierto, pero si quiero verlo debo mirar aquí (P), porque aquí vuelve a aparecer. La continuación de lo que está lejos por ahí se hace sentir aquí. Lo que busco cuando salgo a distancias infinitas, hace su aparición en mi interior y se me manifiesta desde este centro.

Este es el tipo de ideas que deben desarrollar en la medida adecuada. En un sentido formal, parecen lo suficientemente sólidas. Como formas de pensamiento, seguramente no puede haber ninguna objeción a ellas. Sin embargo, se obtendrán resultados verdaderamente notables si con su ayuda intentas penetran la realidad exterior. Piensen, por ejemplo, que podría haber un fenómeno en el espacio celeste, —podemos llamarlo «Luna» para empezar— sin embargo, este fenómeno no debería entenderse simplemente diciendo: «Esta Luna es un cuerpo, aquí está su punto central; lo investigaremos entendiendo que es un cuerpo y que su punto central está aquí». Asumir (y perdón por lo dicho, lo digo eufemísticamente) asumir que esta forma de pensar no encajaba con la realidad, pero que debería expresarla de otra manera. Más bien debería decir: «Si yo, en mi Universo, empiezo desde cierto punto y me alejo más y más, llego a donde ya no encontraré cuerpos celestes. Sin embargo, tampoco encontraré un mero espacio euclidiano vacío. No, encontraré algo cuya realidad inherente me obliga a reconocer la continuación de ello aquí (en P)». Entonces me vería obligado a concebir el espacio contenido dentro de la Luna como una porción de todo el Universo con la excepción de todo lo que existe en forma de estrellas, etc., fuera de la Luna. Debería pensar por un lado en todas las estrellas que están aquí en el espacio cósmico. Ahora supongo que tengo que tratarlas de una manera, de acuerdo con un solo principio; pero el interior de la Luna —el espacio contenido dentro de la Luna— no podría ser tratado de esta manera. Me obligaría a pensar lo siguiente: allí, por un lado, salgo a los espacios lejanos. En algún lugar, supongo, está la Esfera celestial. Aunque sea sólo la Esfera «aparente» para empezar; algo efectivo, algo real debe concebirse para subyacerlo. Sin embargo, independientemente de las realidades que descubra, el espacio dentro de la superficie esférica de la Luna no tiene nada que ver con eso. Solo tiene que ver con lo que comienza donde terminan las estrellas. Es un fragmento, de alguna manera extraña, que no pertenece a mi Universo sino a ese Universo al que no pertenecen todas las estrellas.

Si existe algo así dentro del Universo, es algo insertado en este Universo, por así decirlo ocluido, algo de naturaleza completamente diferente y que revela diferentes propiedades internas de todo lo que hay a su alrededor. Y entonces podemos comparar la relación de tal Luna con los Cielos que la rodean con la relación que se obtiene, por ejemplo, entre las secreciones de los riñones —con la estructura orgánica que los subyace y por otro lado la estructura y funcionamiento de los ojos. De aquí procederemos mañana.

No es debido a mí que deba tratar de formar, y familiarizarlos con, nociones tan complicadas de cómo está construido el Universo. La verdad es que, equipado con cualquier otra noción, no avanzarán, salvo en la convención: «Comprendamos los fenómenos con nuestro rango de ideas dado, y si llegamos a un límite en alguna parte, entonces lo hacemos, y no vamos más lejos». Atribúyanlo entonces a la realidad y no a ningún anhelo de ideas remotas, si en el esfuerzo por impartir una comprensión de cómo está construido el Universo he desarrollado nociones complicadas.

Traducción revisada por Gracia Muñoz en febrero de 2021